TIA. Taller: Límites indeterminados y al infinito

 NOMBRES Y APELLIDOS COMPLETOS: Estefania Agredo Posada- Henry David Blanco- Sebastian Rua 

Escriba en su cuaderno de apuntes o en hojas sueltas, los procedimientos solicitados y escanéelos o tómales fotos para que pueda adjuntarlos como evidencia de su trabajo.

La gráfica de la función f(x) = 1/x es la siguiente Determine: x+f(x) x-f(x) x0f(x) x-1f(x) x1f(x)

2.    La gráfica de la función f(x) = x2 + 2 es las siguiente Determine: x+f(x) x-f(x) x0f(x)

3.   La gráfica de la función f(x) = -x2 - 1  Determine: x+f(x) x-f(x) x0f(x)

4.    La gráfica de la función f(x) = Lnx es la siguiente Determine: x+f(x) x-f(x) x0f(x) x1f(x)

5.   La gráfica de la función f(x) = 2Cosx es la siguiente Determine: x+f(x) x-f(x) x0f(x)

6.   La gráfica de la función f(x) = (x+1)3 es la siguiente Determine: x+f(x) x-f(x) x-1f(x)

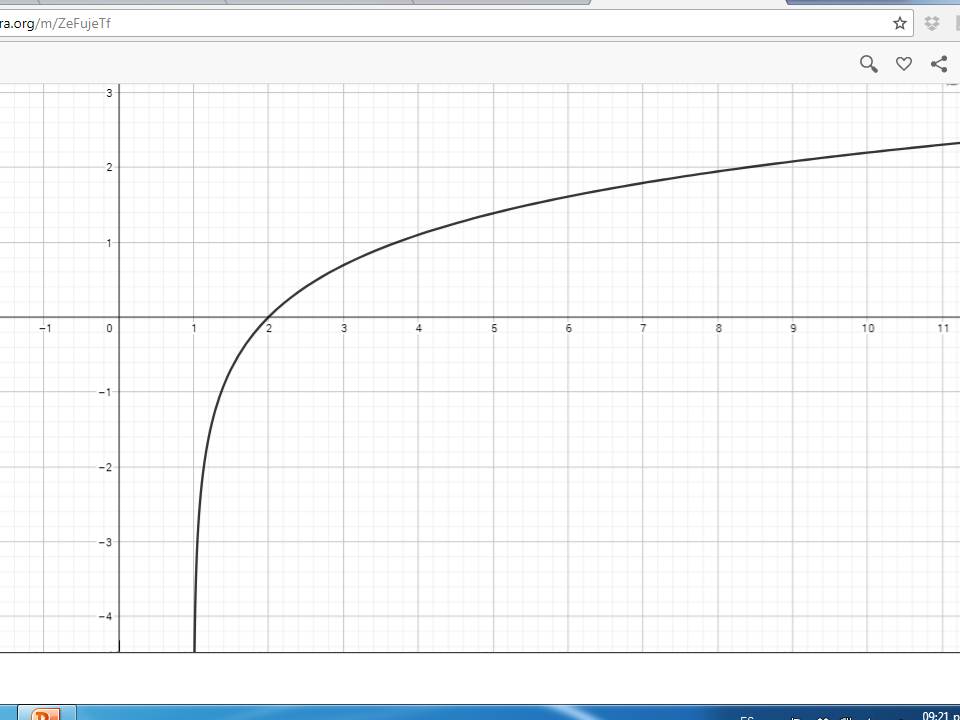
7.   La gráfica de la función f(x) = Ln(x-1) es la siguiente Determine: x+f(x) x-f(x) x1f(x) x2f(x)

8.    La gráfica de la función es la siguiente Determine: x+f(x) x-f(x) x1f(x)

 Calcule los siguientes límites indeterminados

9.    x-2/3(6x2 + 13x + 6) / (9x2 + 4) 

10.  x-2/3(9x2 + 4) / (6x2 + 13x + 6) 

11.   x-4/3(12x2 + 13x - 4) / (15x2 + 29x + 12) 

12.   x-4/3(15x2 + 29x + 12) / (12x2 + 13x - 4) 

13.   x1/4(12x2 + 13x - 4) / (8x2 + 18x - 5) 

14.   x1/4(8x2 + 18x - 5) / (12x2 + 13x - 4) 

Inserte aquí los procedimientos